Die Erklärung des Herstellers ist noch nicht alles. Wie kann man prüfen, ob die Wärmedämmung unsere Erwartungen unter unterschiedlichsten Umgebungsbedingungen erfüllen wird?

Deklarierte und berechnete Wärmedämmungsparameter

Die Darstellung der Wärmedämmungsparameter von Baustoffen beschränkt sich in der Regel auf die Angabe des Lambda-Koeffizienten (Wärmedurchgangskoeffizient - je niedriger dieser Wert ist, desto besser sind die wärmedämmenden Eigenschaften).

Ein Lambdawert und der andere sind aber nicht dasselbe. Es gibt nämlich einen Unterschied zwischen dem deklarierten und dem berechneten Lambdawert. Und dies kann bei der jeweiligen Investition von entscheidender Bedeutung für die Auswahl des wärmedämmenden Materials sein. Viel hängt nämlich ab von den Bedingungen, die auf das jeweilige Objekt einwirken.

Der deklarierte Lambdawert ist ein Kennwert, der unter normativen Bedingungen ermittelt wird. In der Praxis bedeutet dies, dass die Wärmedämmungseigenschaften bei +10 °C ermittelt werden. Die Messungen werden unter Laborbedingungen am neuen, trockenen und spannungsfreien Material durchgeführt.

Der berechnete Lambdawert wird hingegen unter Nutzungsbedingungen ermittelt, d.h. sowohl bei niedrigen als auch bei hohen Umgebungstemperaturen. Der Temperaturbereich beträgt hier von -30 °C bis +60 °C.

Es kann einfach ermittelt werden, wie wirksam die Mineralwolle bei +10 °C und wie wirksam sie bei +50 °C ist, z.B. im Dachgeschoss unter Sonneneinwirkung. Im dargestellten Beispiel hat sich der Lambdawert unter dem Temperatureinfluss von 0,040 W/mK auf 0,050 W/mK geändert. Anders gesagt, verlor die Mineralwolle unter diesen Bedingungen 25% ihrer Wirksamkeit.

Annäherung der Werte über +30 °C

Die Umgebungstemperatur ist nicht der einzige Faktor, der für die Ermittlung des berechneten Lambawertes erforderlich ist. Mehr zu diesem Thema sagt die Norm PN-EN ISO 10456. Die o.g. Norm beschreibt das Problem der allgemeinen und detaillierten Ermittlung physikalischer Größen, mit denen die Eigenschaften von Baustoffen definiert werden.

In diesem Dokument ist die Methode der Konversion (Umrechnung) von Werten, die bei einem bestimmten Satz von Bedingungen erreicht wurden, in Werte, die bei einem anderen Satz gelten, angegeben. Für die Durchführung der Berechnungen müssen Faktoren wie die oben bereits genannte Umgebungstemperatur, die Luftfeuchtigkeit und die Alterung des Materials bekannt sein.

Das Problem besteht drin, dass präzise Berechnungen nur in der Theorie möglich sind. Hersteller wärmeisolierender Stoffe verfügen in der Regel über keine Ergebnisse von Laboruntersuchungen, bei denen der Lambda-Koeffizient für verschiedene Luftfeuchtigkeitswerte definiert worden wäre. Das Gleiche gilt für den Konversionsfaktor hinsichtlich der Alterung.

Bei einem eventuellen Versuch der Ermittlung des berechneten Lambdawertes kann folgende Formel verwendet werden:

λ_obl = λ_D · F_T · F_M · F_A

λ_obl - Berechnungslambdawerte
λ_D - deklarierter Lambdawert
F_M - Konversionsfaktor hinsichtlich der Feuchte
F_A - Konversionsfaktor hinsichtlich der Alterung
F_T - Konversionsfaktor hinsichtlich der Temperatur*

*der Wert von F_T wird folgendermaßen ermittelt:

F_T = e^fT(T2-T1)

e - mathematische Konstante, d.h. 2,72
T1 - Normtemperatur bei der Ermittlung des deklarierten Lambdakoeffizienten, d.h. +10 °C
T2 - Temperatur aus dem anderen Satz Umgebungsbedingungen (z.B. +50 °C)
fT - temperaturbezogener Konversionsfaktor gem. PN-EN ISO 10456 (die Angaben sind der nachfolgend aufgeführten Tabelle zu entnehmen)

 

So viel zur Theorie. Obwohl nicht viele Angaben zum Verhalten von Baustoffen unter der Einwirkung von Feuchte und Alterung zur Verfügung stehen, ist festzustellen, dass die Bedingungen, unter denen die Wärmedämmung stattfindet, von sehr großer Bedeutung sind.

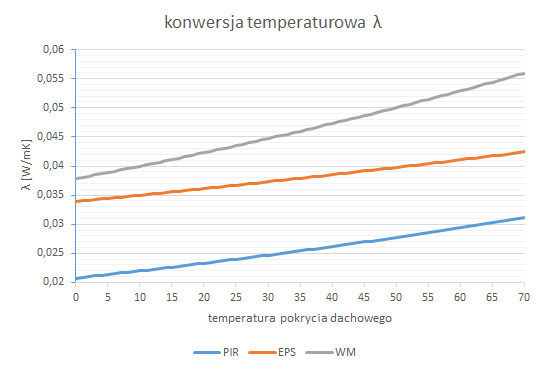
Aus dem Diagramm „Temperaturbezogene Konversion λ" geht hervor, dass von einer steigenden Tendenz des konvertierten Parameters λ am stärksten diffusionsoffene Faserstoffe betroffen sind. Die Tendenz bei EPS-Styropor scheint der Tendenz von PIR-Paneelen ähnlich zu sein (mit einer etwas weniger steigenden Tendenz). Dies ist bei höheren Temperaturen am deutlichsten zu sehen, die für Produkte aus extrudiertem Polystyrol ein gefährliches Niveau erreichen können. Der Grad der Zerstörung von EPS bei Temperaturen um +70 °C ist nicht einschätzbar. Deswegen hat das Konversionsdiagramm von EPS für diesen Temperaturbereich nur theoretischen Charakter.

Unter Berücksichtigung der Berechnungsänderung bei Wärme lässt sich die Dicke der Wärmedämmung bestimmen, durch die dieselbe Wärmedämmung von U_max = 0,18 W/m²K sichergestellt werden kann:

1. Nehmen wir an, dass die durchschnittliche Temperatur der „erhitzten“ Wärmedämmschicht bei +50 °C liegt. Die deklarierten Messungen (λ_D) werden bei +10 °C durchgeführt. Es ist einfach zu errechnen, dass die tatsächliche Temperatur auf dem Dach um 40 °C steigt

2. Aus den oben dargestellten Tabellen sind folgende tabellarische Werte der entsprechenden fT-Koeffizienten ersichtlich: EPS-Styropor - 0,0032, Mineralwolle - 0,0056, PIR-Paneele - 0,0058.

3. Aus den weiteren Berechnungen ergibt sich Folgendes: 

- Konversionsfaktor F_T bei ΔT = 40°C für Styropor EPS = 1,1137
- Konversionsfaktor F_T bei ΔT = 40°C für Mineralwolle = 1,251
- Konversionsfaktor F_T bei ΔT = 40°C für Paneele PIR = 1,261

Aus den o.g. Berechnungen ergibt sich, dass bei der Temperatur, bei der die Wärmedämmung eingesetzt wird, d.h. bei +50 °C, also 40 °C mehr als bei dem deklarierten Lambdawert, die Wärmeleitkoeffizienten folgende Werte aufweisen:

- Styropor EPS λ_EPS+ = 0,035 · 1,137 ≈ 0,040 W/mK
-Mineralwolle λ_MW+ = 0,040 · 1,251 ≈ 0,050 W/mK
- Paneele λ_PIR+ = 0,023 · 1,261 ≈ 0,029 W/mK

 4. Dicke der Wärmedämmung, die erforderlich ist, um den Wert von U_max = 0,18 W/m²K zu erreichen

- EPS-Styropor λ_EPS+ = 0,222 m (222 mm), Steigerung um 14,4%
- Mineralwolle λ_MW+ = 0,278 m (278 mm), Steigerung um 25,2%
- Paneele λ_PIR+ = 0,161 m (161 mm), Steigerung um 25,8%

Aus den obigen Berechnungen ergibt sich, dass zur Gewährleistung eines für den Sommer angenommenen Wärmedämmungsgrades die Montage einer dickeren Schicht Wärmedämmung unter Berücksichtigung der temperaturbezogenen Konversion notwendig ist. Dies ist von enormer Bedeutung bei der Kostenschätzung für die Luftkühlung in klimatisierten Gebäuden.

Analoge Berechnungen für Minustemperaturen würden bei der Ermittlung einer entsprechenden Stärke der Wärmedämmung bei Winterbedingungen helfen. Außerdem könnte man so die Heizkosten für das Gebäude optimieren.