Declared vs. design thermal insulation parameters
- Details
Declarations of thermal insulation manufacturers are not everything. How can we check if the thermal insulation meets our expectations under different environmental conditions?
Declared vs. design thermal insulation parameters
The presentation of the parameters related to thermal insulation construction materials usually boils down to giving the lambda. This is the coefficient of thermal conductivity - where the lower the value, the better the thermal insulation properties.
However, lambda values are not equivalent. There is an important difference between the declared lambda and the design lambda. The latter can be the key to the suitable thermal insulation material for the given project. Much depends on the conditions under which the given structure will be used.
The declared lambda is determined under standard test conditions. In practice, this means that the "thermal insulation" of a material is determined at a temperature of +10°C. Of course, this measurement is performed under laboratory conditions, on fresh, dry and non-stressed material.
The design lambda is determined under operating conditions, i.e. at both low and high ambient temperatures. This covers the range from -30°C to +60°C.
The insulation efficiency of mineral wool at +10°C and at +50°C, such as in a sun-heated attic, can be easily calculated. For this example, the lambda changed from 0.040 W/mK to 0.050 W/mK due to the change in temperature. In other words, under such conditions the thermal insulation efficiency of mineral wool was 25% lower.
Value approximation above +30°C
Ambient temperature is not the only coefficient required to determine the design lambda. More information is available in PN-EN ISO 10456, which documents the area of general and specific definitions for the physical quantities used to describe some of the properties of construction materials.
The standard gives the method of converting the values obtained under one set of conditions to values applicable to another set. These calculations require more coefficients, including the ambient temperature as well as humidity and material ageing.
The problem is that the calculations are mainly theoretical. The manufacturers of thermal insulation materials usually do not have the laboratory test results to confirm the lambda at various humidity values. The same problem applies to the ageing conversion coefficient.
However, to determine the design lambda the following formula can be used:
λobl = λD · FT · FM · FA
λobl - design lambda
λD - declared lambda
FM - humidity conversion coefficient
FA - ageing conversion coefficient
FT - temperature conversion coefficient*
*FT is calculated as follows:
FT = efT(T2-T1)
e - mathematical constant, i.e. 2.72
T1 - standard measurement temperature of the declared lambda, i.e. +10°C
T2 -temperature from the second set of conditions (e.g. +50°C)
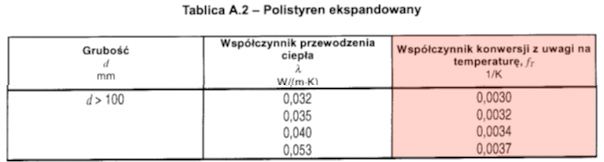
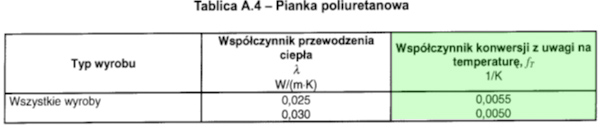
fT - temperature conversion coefficient as per PN-EN ISO 10456 (data in tables below)
So much for the theory. Despite the lack of important data on the behaviour of materials under the impact of humidity and time, the importance of the conditions under which the thermal insulation will be used is clearly visible.
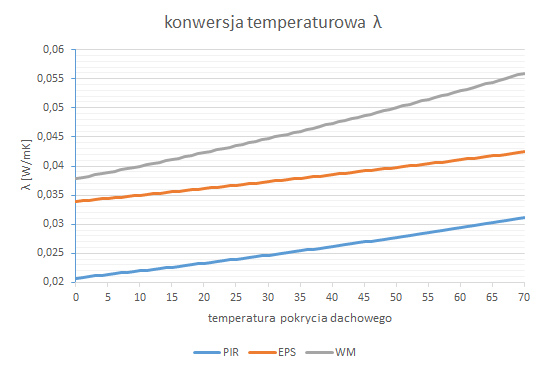
The "λ temperature conversion" diagram shows that the increasing tendency of the λ conversion parameter has the most impact on fibre-based, diffusion-open materials. EPS seems to have a similar tendency to PIR (insignificantly less increase); however it is the most visible at high temperatures, reaching a level dangerous to extruded polystyrene products. The EPS destruction rate at temperatures close to +70°C is impossible to estimate, thus the EPS conversion diagram for these temperatures is only theoretical.
Considering the design variation of the heat parameter, thermal insulation thickness values can be determined where the same thermal insulation efficiency Umax = 0,18 W/m2K will be ensured:
1. Let us assume that the average temperature of a "heated" layer of the thermal insulation on the roof is approximately +50°C. Declared measurements (λD) are made at +10°C. It is easy to calculate that the increase in the real operating temperature on the roof is 40°C.
2.The values of the appropriate fT coefficients can be read from the tables above: EPS - 0.0032, mineral wool - 0.0056, PIR panels - 0.0058.
3. Based on further calculations:
- FT conversion coefficient at ΔT = 40°C for EPS = 1.1137
- FT conversion coefficient at ΔT = 40°C for mineral wool = 1.251
- FTconversion coefficient at ΔT = 40°C for PIR panels = 1.261
Based on the above calculations, at a thermal insulation operating temperature of +50°C, 40°C higher than for the declared lambda, the thermal conductivity coefficients are as follows:
- EPS λEPS+ = 0,035 · 1,137 ≈ 0,040 W/mK
- mineral wool λMW+ = 0,040 · 1,251 ≈ 0,050 W/mK
- PIR panels λPIR+ = 0,023 · 1,261 ≈ 0,029 W/mK
4. Thermal insulation thickness required to obtain Umax = 0,18 W/m2K
- EPS λEPS+ = 0,222 m (222 mm), increased by 14,4%
- mineral wool λMW+ = 0,278 m (278 mm), increased by 25,2%
- PIR panels λPIR+ = 0,161 m (161 mm), increased by 25,8%
Based on the above calculations for temperature conversions, to ensure the assumed thermal insulation efficiency level in summer, a thicker thermal insulation layer must be installed. This is essential in estimating the air cooling costs in air-conditioned buildings.
By analogy, calculations for negative temperatures are helpful in the estimation of the thermal insulation thickness for winter conditions and the impact on heating cost optimisation.





Your reply